- 全部分类/
- 教育教学/
- 数理天地(初中版)
 扫码免费借阅
扫码免费借阅
目录
快速导航-
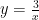
基础精讲 | 反比例函数中面积问题的解决策略
基础精讲 | 反比例函数中面积问题的解决策略
-
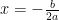
基础精讲 | 初中二次函数含参问题中参数变化规律与解题模型构建研究
基础精讲 | 初中二次函数含参问题中参数变化规律与解题模型构建研究
-
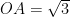
基础精讲 | 直线与圆的位置关系及其应用探究
基础精讲 | 直线与圆的位置关系及其应用探究
-
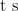
基础精讲 | 动态几何视角下相似三角形的多解性问题探究
基础精讲 | 动态几何视角下相似三角形的多解性问题探究
-
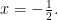
基础精讲 | 抓定促变,分类求解
基础精讲 | 抓定促变,分类求解
-
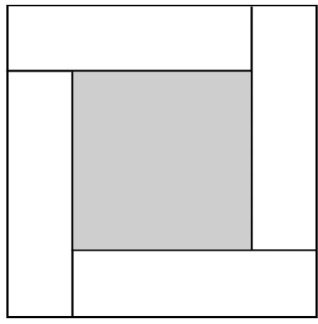
例题精讲 | 基于APOS理论的初中数学深度学习的教学设计
例题精讲 | 基于APOS理论的初中数学深度学习的教学设计
-
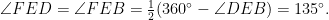
例题精讲 | 无中猜想,别出机杼
例题精讲 | 无中猜想,别出机杼
-
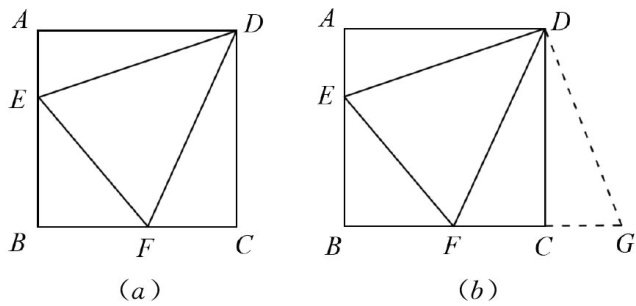
例题精讲 | 示例解析挖掘,模型探究指导
例题精讲 | 示例解析挖掘,模型探究指导
-
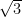
例题精讲 | 平面直角坐标系中直线与等边三角形综合问题解析
例题精讲 | 平面直角坐标系中直线与等边三角形综合问题解析
-

例题精讲 | 二次函数与几何综合问题解析
例题精讲 | 二次函数与几何综合问题解析
-

例题精讲 | 从一题多解到创新思维的培养
例题精讲 | 从一题多解到创新思维的培养
-

例题精讲 | 例谈二次函数在求解最值问题中的应用
例题精讲 | 例谈二次函数在求解最值问题中的应用
-
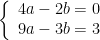
例题精讲 | 二次函数与平行四边形存在性问题的探究
例题精讲 | 二次函数与平行四边形存在性问题的探究
-
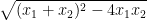
解题技巧 | 初中数学大单元设计解题策略探析
解题技巧 | 初中数学大单元设计解题策略探析
-
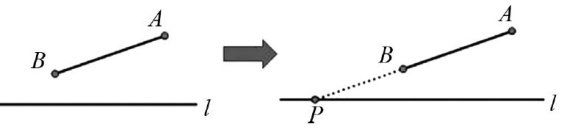
解题技巧 | 函数背景下的线段差最值解法探究
解题技巧 | 函数背景下的线段差最值解法探究
-
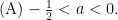
解题技巧 | 擷谈代数推理题教学的“三增”之效
解题技巧 | 擷谈代数推理题教学的“三增”之效
-
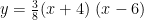
解题技巧 | 二次函数与几何综合题的解题策略
解题技巧 | 二次函数与几何综合题的解题策略
-
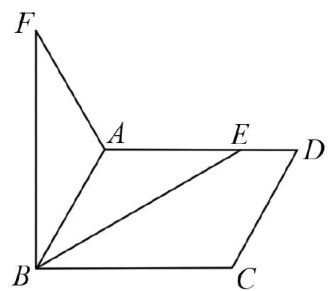
解题技巧 | 浅谈单线段最小值的解题策略
解题技巧 | 浅谈单线段最小值的解题策略
-

解题技巧 | 初中数学课堂解题中数形结合方法的实践和思考
解题技巧 | 初中数学课堂解题中数形结合方法的实践和思考
-
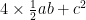
解题技巧 | 初中数学几何图形证明题的解题策略
解题技巧 | 初中数学几何图形证明题的解题策略
-
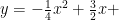
解题技巧 | 二次函数与三角形相关问题的探究
解题技巧 | 二次函数与三角形相关问题的探究
-
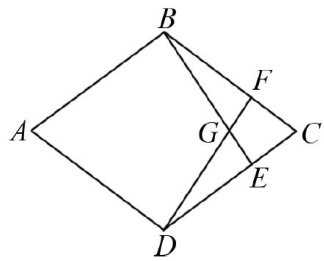
解题技巧 | 初中数学几何证明题的常见解题策略与思维培养研究
解题技巧 | 初中数学几何证明题的常见解题策略与思维培养研究
-

聚焦“双减” | “双减”背景下初中数学分层作业设计与解题能力提升
聚焦“双减” | “双减”背景下初中数学分层作业设计与解题能力提升
-
聚焦“双减” | “双减"背景下初中数学作业提质增效策略研究
聚焦“双减” | “双减"背景下初中数学作业提质增效策略研究
-
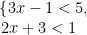
聚焦“双减” | “双减”背景下初中数学教学开放式课堂构建
聚焦“双减” | “双减”背景下初中数学教学开放式课堂构建
-
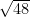
聚焦“双减” | “双减”政策下初中数学作业设计与实践分析
聚焦“双减” | “双减”政策下初中数学作业设计与实践分析
-

聚焦“双减” | “双减”背景下初中数学课堂巧设教学情境初探
聚焦“双减” | “双减”背景下初中数学课堂巧设教学情境初探
-
优化课堂方法 | 初中数学探究式活动课实践与思考
优化课堂方法 | 初中数学探究式活动课实践与思考
-

优化课堂方法 | 初中数学课堂互动教学的构建与实施策略
优化课堂方法 | 初中数学课堂互动教学的构建与实施策略
-

优化课堂方法 | 问题导学模式在初中数学课教学中的应用
优化课堂方法 | 问题导学模式在初中数学课教学中的应用
-
优化课堂方法 | 初中数学单元结构化教学的深化探索
优化课堂方法 | 初中数学单元结构化教学的深化探索
-
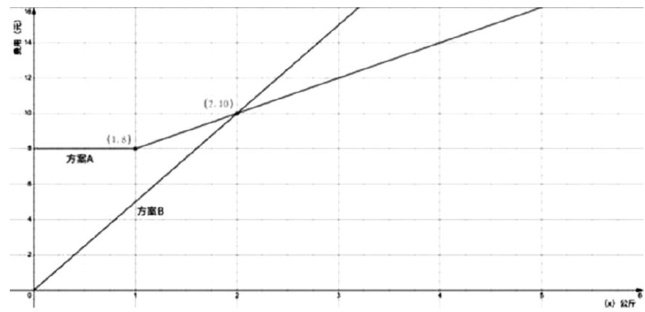
优化课堂方法 | 任务驱动教学法在初中数学教学中的应用
优化课堂方法 | 任务驱动教学法在初中数学教学中的应用
-
优化课堂方法 | 基于差异化任务的初中数学教学评价体系优化
优化课堂方法 | 基于差异化任务的初中数学教学评价体系优化
-
优化课堂方法 | 以问导思
优化课堂方法 | 以问导思
-
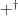
优化课堂方法 | 基于初中数学“链十"课程的创造能力提升
优化课堂方法 | 基于初中数学“链十"课程的创造能力提升
-
优化课堂方法 | 初中数学错题资源在个性化教学中的运用路径
优化课堂方法 | 初中数学错题资源在个性化教学中的运用路径
-

教学思想实践 | 数学素养导向下教学目标的定位与实践
教学思想实践 | 数学素养导向下教学目标的定位与实践
-

教学思想实践 | 数形结合思想在初中教学中的深度融合策略
教学思想实践 | 数形结合思想在初中教学中的深度融合策略
-
教学思想实践 | 初中数学“教学评”一体化的构建与实践
教学思想实践 | 初中数学“教学评”一体化的构建与实践
-
教学思想实践 | 初中数学教学中的项目式学习设计与实施
教学思想实践 | 初中数学教学中的项目式学习设计与实施
-
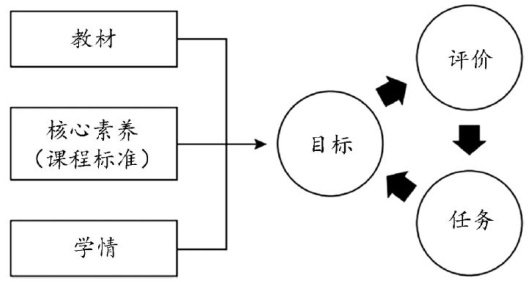
教学思想实践 | 新课标下初中数学“教一学一评”一致性的策略研究
教学思想实践 | 新课标下初中数学“教一学一评”一致性的策略研究
-

教学思想实践 | 初中函数概念教学中“变化”思想的渗透策略研究
教学思想实践 | 初中函数概念教学中“变化”思想的渗透策略研究
-
教学思想实践 | 初中数学项目化学习实践研究
教学思想实践 | 初中数学项目化学习实践研究
-
教学思想实践 | 新课标背景下初中数学“教一学一评”一致性探讨
教学思想实践 | 新课标背景下初中数学“教一学一评”一致性探讨
-
教学思想实践 | 初中数学跨学科主题学习的设计与实施探究
教学思想实践 | 初中数学跨学科主题学习的设计与实施探究
-

教学经验交流 | 基于项目式学习的初中数学单元整体教学设计案例开发
教学经验交流 | 基于项目式学习的初中数学单元整体教学设计案例开发
-

教学经验交流 | 巧用几何画板,助力初中数学教学
教学经验交流 | 巧用几何画板,助力初中数学教学
-
教学经验交流 | 基于错题资源的初中数学精准化教学策略研究
教学经验交流 | 基于错题资源的初中数学精准化教学策略研究
-

教学经验交流 | 项目式教学在初中数学概率与统计板块的应用路径
教学经验交流 | 项目式教学在初中数学概率与统计板块的应用路径
-
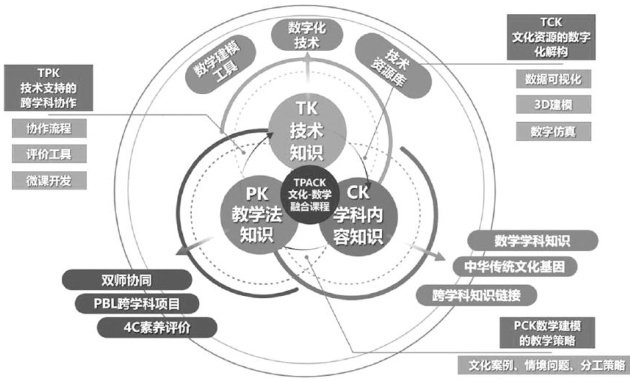
教学经验交流 | 基于4C一TPACK框架的初中数学跨学科项目式学习设计研究
教学经验交流 | 基于4C一TPACK框架的初中数学跨学科项目式学习设计研究
-
教学经验交流 | 基于立德树人推进初中数学教育高质量发展实践
教学经验交流 | 基于立德树人推进初中数学教育高质量发展实践
-

教学经验交流 | 新课标视域下初中数学跨学科教学的实施策略
教学经验交流 | 新课标视域下初中数学跨学科教学的实施策略
-
教学经验交流 | 中考数学复习课教学路径建构的策略与反思
教学经验交流 | 中考数学复习课教学路径建构的策略与反思
-

教学经验交流 | 探讨函数概念在初中数学课程中的引入与理解途径
教学经验交流 | 探讨函数概念在初中数学课程中的引入与理解途径
-
核心素养培养 | 让学习真实发生
核心素养培养 | 让学习真实发生
-
核心素养培养 | 初中数学深度教学与学生数学素养的提升
核心素养培养 | 初中数学深度教学与学生数学素养的提升
-
学生培养研究 | 初中数学教学中培养学生思维品质的策略
学生培养研究 | 初中数学教学中培养学生思维品质的策略
-

学生培养研究 | 指向学生深度学习的初中数学课堂教学实践探究
学生培养研究 | 指向学生深度学习的初中数学课堂教学实践探究
-
学生培养研究 | 初中数学教学中培养学生数学思维能力的措施探讨
学生培养研究 | 初中数学教学中培养学生数学思维能力的措施探讨
-
学生培养研究 | 指向逆向思维能力培养的初中数学教学实践分析
学生培养研究 | 指向逆向思维能力培养的初中数学教学实践分析
-
学生培养研究 | 初中数学不等式教学的类比式路径研究
学生培养研究 | 初中数学不等式教学的类比式路径研究
-

学生培养研究 | 初中数学建模教学中数据处理能力提升策略研究
学生培养研究 | 初中数学建模教学中数据处理能力提升策略研究
-
教师成长之路 | 基于动态数学工具的初中教师数学实验课教学能力提升策略
教师成长之路 | 基于动态数学工具的初中教师数学实验课教学能力提升策略
-
教育技术与数学融合 | 智慧云平台在初中数学混合式教学实践中的应用
教育技术与数学融合 | 智慧云平台在初中数学混合式教学实践中的应用
-
教育技术与数学融合 | 基于AI技术的初中数学新型数字化教学模式研究
教育技术与数学融合 | 基于AI技术的初中数学新型数字化教学模式研究
-
教育技术与数学融合 | 人工智能与初中数学特色课程融合创新应用研究
教育技术与数学融合 | 人工智能与初中数学特色课程融合创新应用研究
过往期刊
更多-

数理天地(初中版)
2025年23期 -

数理天地(初中版)
2025年22期 -

数理天地(初中版)
2025年21期 -

数理天地(初中版)
2025年20期 -

数理天地(初中版)
2025年19期 -

数理天地(初中版)
2025年18期 -

数理天地(初中版)
2025年17期 -

数理天地(初中版)
2025年16期 -

数理天地(初中版)
2025年15期 -

数理天地(初中版)
2025年14期 -

数理天地(初中版)
2025年13期 -

数理天地(初中版)
2025年12期 -

数理天地(初中版)
2025年11期 -

数理天地(初中版)
2025年10期 -

数理天地(初中版)
2025年09期 -

数理天地(初中版)
2025年08期 -

数理天地(初中版)
2025年07期 -

数理天地(初中版)
2025年06期 -

数理天地(初中版)
2025年05期 -

数理天地(初中版)
2025年04期 -

数理天地(初中版)
2025年03期 -

数理天地(初中版)
2025年02期 -

数理天地(初中版)
2025年01期










 登录
登录